The new cohort of Getting Started With Python for Quant Finance is open!

When you're ready, here's what you get:

•  10 live sessions where you'll install and configure Python, create a quant lab in Jupyter Notebook, install packages, understand the quant finance landscape, and build real quant code.

•  The 10-module curriculum you can review at your own pace (with lifetime access to these recordings)

•  20 Jupyter Notebooks with real quant code you can use immediately

•  Lifetime access to session recordings with detailed show notes, resources, and transcripts

•  Weekly Q&A sessions to reinforce everything you’ve learned (and make sure nobody gets left behind)

•  Private community of beginners with channels for different topics, platforms, niches, and geographies

•  3 step-by-step guides making sure you always have high-value problems to solve, know exactly how to get started with Python, and how to ask questions to get great answers from the community to get unstuck fast

•  [BONUS]: Deep Dive into OpenBB - the FREE, open-source, Bloomberg Terminal with the founder and CEO

•  [BONUS]: A free copy of The Ultimate Guide to Pricing Options and Implied Volatility with Python

• ️ [BONUS]: A top spot on the waiting list for Trade Blotter along with a 50% discount for lifetime access.

•  [BONUS]: Free copy of the Options Breakeven Cheat Sheet

Finally get out of Tutorial Hell.

Now, on to the newsletter!

In today’s issue, I’m going to show you how to beta-hedge a stock portfolio against a benchmark.

Portfolio managers talk a lot about alpha. Alpha is the return they earn above and beyond the market benchmark they’re measured against. Alpha matters because managers are paid to outperform the benchmark.

If alpha is the return they earn above and beyond the market, beta is the return they earn by being exposed to the market.

Beta hedging concentrates exposure to alpha

Portfolio managers design factor models that tell them how to balance a portfolio to earn alpha. Because alpha is how managers get paid, they only want exposure to their factors. Beta hedging removes the part of returns driven by the market and leaves only the returns driven by the factors.

If this sounds complicated there’s good news: You can hedge beta with the same linear regression you learned in Statistics 101. And you can do it with Python.

By the end of this issue, you’ll know how to:

1. Get data for stock and benchmark
2. Find a portfolio’s alpha and beta
3. Hedge beta

Step 1: Get the data

Start by importing the libraries. statsmodels is a package used to build statistical models like linear regression.

1import numpy as np
2from statsmodels import regression
3import statsmodels.api as sm
4import matplotlib.pyplot as plt
5import yfinance as yf

Next, get the data. I use TSLA as an example of a stock portfolio. You can use actual portfolio returns instead.

1data = yf.download("TSLA, SPY", start="2014-01-01", end="2015-01-01")
2
3asset = data["Adj Close"].TSLA
4benchmark = data["Adj Close"].SPY

Finally, get the returns and plot them.

1asset_returns = asset.pct_change().dropna()
2benchmark_returns = benchmark.pct_change().dropna()
3
4asset_returns.plot()
5benchmark_returns.plot()
6plt.ylabel("Daily Return")
7plt.legend()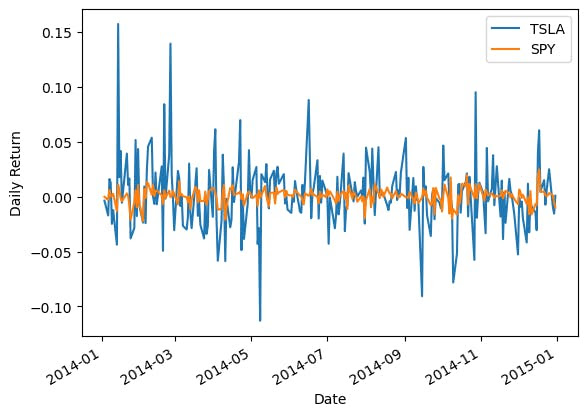

Step 2: Find the portfolio’s alpha and beta

Linear regression models have an alpha term and one or more beta terms (plus an error). Alpha is the intercept and beta is the slope of the line that minimizes the error between all the points on a scatter plot. This will be clear when you see the chart.

But first, build the code.

1X = benchmark_returns.values
2Y = asset_returns.values
3
4def linreg(x, y):
5    # Add a column of 1s to fit alpha
6    x = sm.add_constant(x)
7    model = regression.linear_model.OLS(y, x).fit()
8    # Remove the constant now that we're done
9    x = x[:, 1]
10    return model.params[0], model.params[1]
11
12alpha, beta = linreg(X, Y)
13print(f"Alpha: {alpha}")
14print(f"Beta: {beta}")

Linreg accepts two inputs: the independent variable (market returns) and the dependent variable (portfolio returns). Inside the function, add a column of 1s so statsmodels can find the alpha term. Then run the model and return the alpha and beta.

The alpha should be near 0. This means that by owning TSLA alone, you’re not beating the benchmark. The beta is 1.95. This means for every 1% the benchmark moves, TSLA moves 1.95% in the same direction.

Plot the returns and the regression line.

1X2 = np.linspace(X.min(), X.max(), 100)
2Y_hat = X2 * beta + alpha
3
4# Plot the raw data
5plt.scatter(X, Y, alpha=0.3)
6plt.xlabel("SPY Daily Return")
7plt.ylabel("TSLA Daily Return")
8
9# Add the regression line
10plt.plot(X2, Y_hat, 'r', alpha=0.9);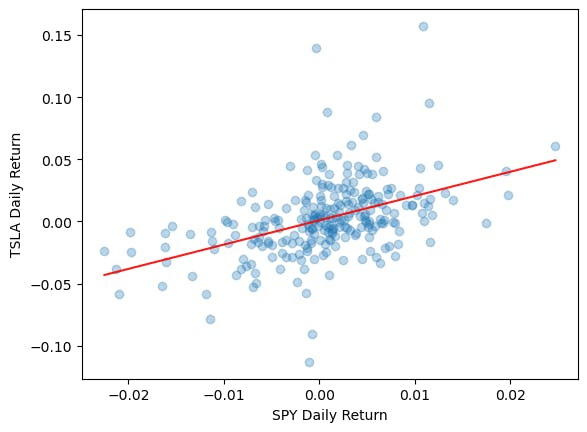

When SPY’s returns are 0, TSLA’s returns are near 0 too. That’s the intercept (alpha). The slope (beta) is measured by the change in TSLA divided by the change in SPY of the red line which is 1.95.

Step 3: Hedge beta

Because you’re only interested in exposure to the returns generated by owning TSLA, hedge the beta. Hedging beta will result in a portfolio with returns close to 0 because alpha is close to 0.

The first step is to construct a beta-hedged portfolio.

1portfolio = -1 * beta * benchmark_returns + asset_returns
2portfolio.name = "TSLA + Hedge"

This says “be short a number of shares in the market equal to the beta plus TSLA.”

Since we’re beta hedged (market neutral) you should expect that the portfolio returns closely resemble that of TSLA. In other words, your exposure is concentrated in your source of alpha.

1portfolio.plot(alpha=0.9)
2benchmark_returns.plot(alpha=0.5);
3asset_returns.plot(alpha=0.5);
4plt.ylabel("Daily Return")
5plt.legend();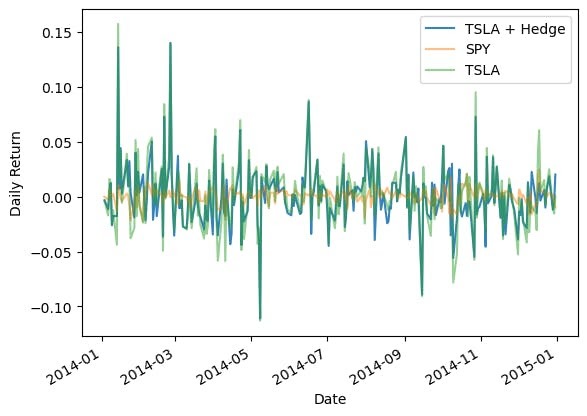

It looks like the portfolio return follows the asset. Run the regression the the portfolio to make sure you removed the beta while keeping the alpha.

1P = portfolio.values
2alpha, beta = linreg(X, P)
3print(f"Alpha: {alpha}")
4print(f"Beta: {beta}")

Sure enough, the beta is 0. You’re hedged!

​

Well, that's it for today. I hope you enjoyed it.

See you again next week.